三角関数#

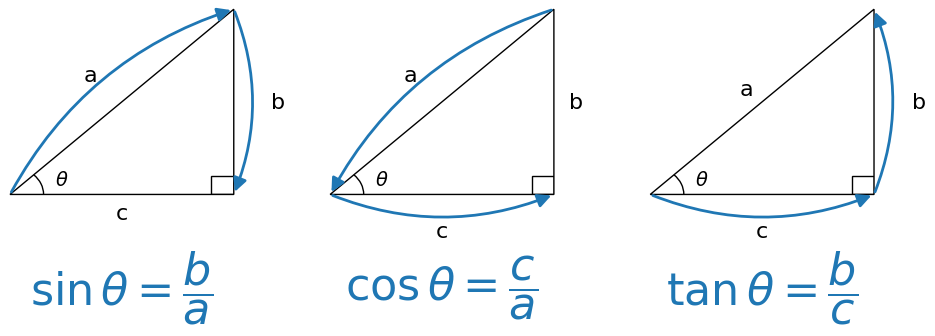
三角形の辺の比による定義#

import numpy as np
import numpy.linalg as LA # 行列計算のため
import matplotlib.pyplot as plt
import matplotlib.patches as pat # 図形描画のため

def my_triangle(ax, points, arrow, label):
  # 三角形
  patch = pat.Polygon(xy=points, fill=False, clip_on=False)
  ax.add_patch(patch)

  # 角マーク
  ang = 45
  arc = pat.Arc(xy=points[0, :], width=0.3, height=0.3, theta1=0, theta2=ang)
  ax.add_patch(arc)

  # 角度ラベル
  ax.annotate(r'$\theta$', xy=points[0, :], xytext=points[0, :]+np.array([0.2, 0.05]), size=14)

  # 直角マーク
  rec_size = 0.1
  rec = pat.Rectangle(xy=points[1, :]-np.array([rec_size, 0]), width=rec_size, height=rec_size, fill=False)
  ax.add_patch(rec)

  # 辺ラベル
  for p1_num, p2_num, arrow, text in arrows:
    # 辺を描くための２点
    p1 = points[p1_num, :]
    p2 = points[p2_num, :]
    
    # 辺p1p2の中点
    p4 = p1+(p2-p1)/2 
    # 辺Cp1を左に90度回転させた点
    p5 = np.array([[0, -1],[1, 0]]) @(p2-p4) + p4 

    # 辺ラベル
    if arrow:
      p5 = (p5-p4)/LA.norm(p5-p4)*0.2 + p4
    else:
      p5 = (p5-p4)/LA.norm(p5-p4)*0.1 + p4
    ax.text(*p5, text, size=16,
            horizontalalignment='center', verticalalignment='center')

    # 辺矢印
    if arrow:
      ax.annotate('', xy=p1, xytext=p2, arrowprops=dict(
          arrowstyle=arrow,
          linewidth=2, # width
          mutation_scale=20, # head size
          connectionstyle="arc3,rad=0.2",
          color='tab:blue'
          ), annotation_clip=False)

  ax.text(0.5, -0.5, label,
          size = 32,
          color = 'tab:blue',
          horizontalalignment='center', verticalalignment='center')

  # 枠を消す
  ax.axis("off")

fig, ax = plt.subplots(1, 3, figsize=(10,5))

## sin
points = np.array([
    [0, 0],
    [1, 0],
    [1, 1]
])
arrows = [
    [1, 0, None, 'c'],
    [2, 1, '<|-', 'b'],
    [0, 2, '<|-', 'a']
]
label = r'$\sin \theta = \dfrac{b}{a}$'
my_triangle(ax[0], points, arrows, label)

## cos
points = np.array([
    [0, 0],
    [1, 0],
    [1, 1]
])
arrows = [
    [1, 0, '-|>', 'c'],
    [2, 1, None, 'b'],
    [0, 2, '-|>', 'a']
]
label = r'$\cos \theta = \dfrac{c}{a}$'
my_triangle(ax[1], points, arrows, label)

## tan
points = np.array([
    [0, 0],
    [1, 0],
    [1, 1]
])
arrows = [
    [1, 0, '-|>', 'c'],
    [2, 1, '-|>', 'b'],
    [0, 2, None, 'a']
]
label = r'$\tan \theta = \dfrac{b}{c}$'
my_triangle(ax[2], points, arrows, label)

fig.tight_layout(pad = 3.0)
plt.show()
../_images/trigonometric_1_0.png

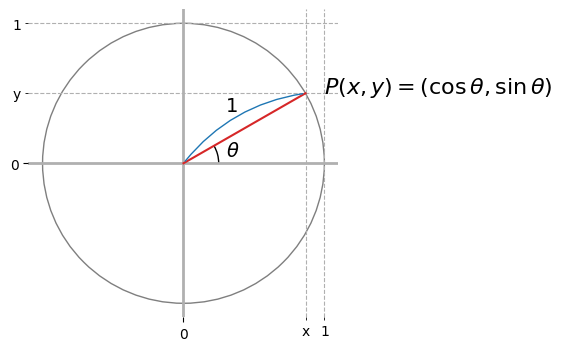
単位円による定義#

単位円上の点\(P(x,y)\)と\(x\)軸の作る角\(\theta\)を使うと、三角関数は以下のように表せられる。

import numpy as np
import numpy.linalg as LA # 行列計算のため
import matplotlib.pyplot as plt
import matplotlib.patches as pat # 図形描画のため

radius = 1.0
angle = 30
theta = np.deg2rad(angle)
x = np.cos(theta)*radius
y = np.sin(theta)*radius

fig, ax = plt.subplots(figsize=(4,4))

# 円
circle = pat.Circle(xy=(0,0), radius=radius, fill=False, color='tab:gray')
ax.add_patch(circle)

# 斜線
ax.plot([0,x], [0,y], color='tab:red')

# 角マーク
size = 0.5
arc = pat.Arc(xy=(0,0), width=size, height=size, theta1=0, theta2=angle)
ax.add_patch(arc)
ax.annotate(r'$\theta$', xy=(0, 0), xytext=(0, 0)+np.array([0.3, 0.05]), size=14)

# 半径 annotation
ax.annotate('', arrowprops=dict(
                arrowstyle='-',
                connectionstyle="arc3,rad=0.2",
                color='tab:blue'
            ),
            xy=(0, 0), xytext=(x, y),
            annotation_clip=False)
ax.text(x=x*0.35, y=y*0.75, s=1, size=14)
# 点P annotation
ax.annotate(r'$P(x,y)=(\cos \theta, \sin \theta)$',
            size=16, 
            xy=(x, y), xytext=(1, y),
            annotation_clip=False)

# 軸
ax.set_xticks([0])
ax.set_xticks([x, 1], minor=True)
ax.set_xticklabels(['x', 1], minor=True)
ax.set_yticks([0])
ax.set_yticks([y, 1], minor=True)
ax.set_yticklabels(['y', 1], minor=True)
ax.set_xlim(-1.1, 1.1)
ax.set_ylim(-1.1, 1.1)
ax.grid(linewidth=2)
ax.grid(which='minor', linestyle='--')

# 枠を消す
# ax.axis("off")
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)


plt.show()
../_images/trigonometric_3_0.png
\[\begin{split} \sin \theta = y\\ \cos \theta = x\\ \tan \theta = \dfrac{y}{x} = \dfrac{\sin \theta}{\cos \theta} \end{split}\]

Note

sin(正弦)…正角（注目している角）に対する弦の長さ
cos(余弦)…余角（正角・直角以外の角）に対する弦の長さ
tan(正接)…正角に対する接線の長さ

公式#

\[\begin{split} \sin^2 \theta + \cos^2 \theta = 1\\ \tan^2 \theta + 1 = \dfrac{1}{\cos^2 \theta}\\ \end{split}\]

導出は、

  • 円の方程式\(x^2+y^2=1\)に\(x=\cos \theta\), \(y=\sin \theta\)を代入

  • \(\sin^2 \theta+\cos^2 \theta=1\)を\(\cos^2 \theta\)を割る

\[\begin{split} \sin(90^{\circ}-\theta)=\cos \theta\\ \sin(90^{\circ}+\theta)=\cos \theta\\ \sin(180^{\circ}+\theta)=-\sin \theta \end{split}\]
\[\begin{split} \cos(90^{\circ}-\theta)=\sin \theta\\ \cos(90^{\circ}+\theta)=-\sin \theta\\ \cos(90^{\circ}+\theta)=-\cos \theta \end{split}\]

加法定理#

\[ \begin{align}\begin{aligned}\begin{split} \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta\\\end{split}\\\begin{split}\sin(\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta\\\end{split}\\\begin{split}\cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta\\\end{split}\\\begin{split}\cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta\\\end{split}\\\begin{split}\tan(\alpha + \beta) = \dfrac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta}\\\end{split}\\\begin{split}\tan(\alpha - \beta) = \dfrac{\tan \alpha - \tan \beta}{1+\tan \alpha \tan \beta}\\ \end{split}\end{aligned}\end{align} \]

導出#

正弦定理#

角と正弦と、外接円の半径の関係式

\(\triangle ABC\)において\(AB=c, BC=a, CA=b\)とする。
\(\angle ABC=B, \angle BCA=C, \angle CAB=A\)とする。
\(\triangle ABC\)の外接円の半径を\(R\)とする。

\[ \dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R \]

例題：１角２辺の情報から他辺を求める#

a = 4, A = 30º, B = 105º のとき、c の値を求めよ。
– スタディクラブ

\[\begin{split} \angle C = 180^{\circ} - (30+105) = 45^{\circ}\\ \end{split}\]

正弦定理より、

\[\begin{split} \dfrac{a}{\sin A} = \dfrac{c}{\sin C}\\ = \dfrac{4}{\sin 30^{\circ}} = \dfrac{c}{\sin 45^{\circ}}\\ \therefore c = \dfrac{4}{\sin 30^{\circ}}\times \sin 45^{\circ}\\ = \dfrac{4\cdot 2}{\sqrt{2}}\\ = 4 \sqrt{2} \end{split}\]

余弦定理#

隣接する２辺の長さとその間の角、残りの辺の長さの関係式。

\(\triangle ABC\)において\(AB=c, BC=a, CA=b\)とする。
\(\angle ABC=B, \angle BCA=C, \angle CAB=a\)とする。

\[\begin{split} c^2 = a^2 + b^2 - 2ab \cos C\\ a^2 = b^2 + c^2 - 2bc \cos A\\ b^2 = c^2 + a^2 - 2ca \cos B \end{split}\]

例題：２辺１角の情報から他辺を求める#

\(a = 3, b = 5, C = 60^{\circ}\) のとき、\(c\) を求めよ。
– スタディクラブ

\[\begin{split} c^2=a^2+b^2-2ab \cos Cより、\\ c^2 = 3^2+5^2-2\cdot 3 \cdot 5 \cdot \cos 60^{\circ}\\ =9+25-30 \dfrac{1}{2}\\ =34-15\\ = 19\\ \therefore c = \sqrt{19} \end{split}\]

極限#

\[\begin{split} \lim_{x\to 0}\dfrac{\sin x}{x}=1\\ \lim_{x\to 0}\dfrac{x}{\sin x}=1\\ \lim_{x\to 0}\dfrac{\tan x}{x}=1\\ \lim_{x\to 0}\dfrac{x}{\tan x}=1\\ \lim_{x\to 0}\dfrac{1- \cos x}{x^2}=\dfrac{1}{2}\\ \lim_{x\to 0}\dfrac{x^2}{1- \cos x}=2\\\end{split}\]

微分#

\[\begin{split} (\sin x)' = \cos x\\ (\cos x)' = -\sin x\\ (\tan x)' = \dfrac{1}{\cos^2 x} \end{split}\]

導出#

\[ (\sin x)' = \lim_{h \to 0} \dfrac{\sin(x+h) - \sin x}{h} \]

加法定理\(\sin(x+\alpha)=\sin x \cos \alpha + \cos x \sin \alpha\)を使って

\[ \begin{align}\begin{aligned}\begin{split} (\sin x)' = \lim_{h \to 0} \dfrac{\sin x \cos h + \cos x \sin h - \sin x}{h}\\ \lim_{h \to 0} \dfrac{\sin x (\cos h -1) + \cos x \sin h}{h}\\\end{split}\\\begin{split}\lim_{h \to 0} \dfrac{\sin x (\cos h -1) }{h} + \dfrac{\cos x \sin h}{h}\\\end{split}\\\begin{split}\lim_{h \to 0} \dfrac{1 - \cos h}{h^2}(- h \sin x) + \dfrac{\sin h}{h}\cos x\\ \end{split}\end{aligned}\end{align} \]

ここで極限の公式 \(\lim_{x\to 0}\dfrac{\sin x}{x}=1\), \(\lim_{x\to 0}\dfrac{1- \cos x}{x^2}=\dfrac{1}{2}\)を使うと、

\[\begin{split} (\sin x)' = \dfrac{1}{2} \cdot 0 + 1 \cdot \cos x\\ =\cos x \end{split}\]

よって \((\sin x)' = \cos x\)が導かれる。